forceflow
New Member
If the facts don't fit the theory, change the facts.
Posts: 29
|
Post by forceflow on Jan 31, 2006 19:06:30 GMT 1
Er zijn te weinig vectoren, dus ze breiden uit met GS. ik kom echter voor u2 [2/wortel(5) 1/wortel(5) 0 ] uit. Wat loopt er mis ? Volg even mee: Voor mij zijn dit de oplossingen van die vergelijking -x1 + 2x2 + 2x3: 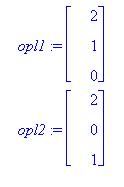 Ik doe vervolgens Graham Schmidt: opl1 - [(opl1 . u1)/(u1 .u1)] . u1 Dit tweede stuk = 0 (nogal logisch, want opl1 staat automatisch loodrecht op u1). Vervolgens normaliseer ik door te delen door wortel 5. |
|
quetzl
~Machines~ 
~Machine 2~
Posts: 168
|
Post by quetzl on Jan 31, 2006 19:15:53 GMT 1
Het is niet fout enkel moet je gewoon uw opl1 als eerste oplossing vastleggen en gram schmidt toepassen om de 2de loodrecht te krijgen op de eerste. Je gaat wel twee andere vecotren krijgen dan gegeven maar dat maakt niet uit omdat die toch wegvallen met de nullen uit de sigma. Ik zou gewoon al meteen 2 loodrechte vectoren zoeken (op elkaar) in plaats van gram schmidt toe te passen, maar doe zoals je wil  . |
|
forceflow
New Member
If the facts don't fit the theory, change the facts.
Posts: 29
|
Post by forceflow on Jan 31, 2006 19:17:33 GMT 1
Als ik oplossing 1 als eerste oplossing vastleg en normaliseer, dan kom ik toch nog niet uit wat zij daar doen ?
En wat jij bedoelt is dan gewoon opl2 - [(opl2 . opl 1)/(opl1 . opl1)].opl1 - [(opl2 . u1)/(u1 . u1)].u1 doen ?
|
|
quetzl
~Machines~
~Machine 2~
Posts: 168
|
Post by quetzl on Jan 31, 2006 19:21:09 GMT 1
nee maar in een driedimensionale ruimte is er meer dan 1 mogelijkheid om zo'n vectoren te vinden.
Neem nu (1,0,0) als 1ste richting
loodrechte koppels zijn:
(0,1,0),(0,0,1)
(0,1,1),(0,1,-1)
enzovoort
|
|
forceflow
New Member
If the facts don't fit the theory, change the facts.
Posts: 29
|
Post by forceflow on Jan 31, 2006 19:23:15 GMT 1
Is dit dan juist voor die tweede vector (u3)
opl2 - [(opl2 . opl 1)/(opl1 . opl1)].opl1 - [(opl2 . u1)/(u1 . u1)].u1 doen ?
|
|
quetzl
~Machines~
~Machine 2~
Posts: 168
|
Post by quetzl on Jan 31, 2006 19:58:42 GMT 1
Dat deel met u1 moet er niet bij he want je hebt hem zoiezo al loodrecht op u1 gekozen door te zeggen dat het een oplossing moet zijn van -x1 + 2x2 + 2x3. Of wist je niet waar dat van kwam dat is gewoon (-1, 2, 2)*(x1,x2,x3), gewoon het inwendig product van u1 met die te zoeken vector.
|
|
